Numerical methods topics:

• Introduction - errors
• Root-finding
• Interpolation
• Numerical integration
• 1st order differential equations
• 2nd order differential equations
• Linear systems
• Finite difference methods
• The Duffing equation
• Approximation of functions
• The numerical evaluation of mathematical functions
• Special inverse functions
• The derivation of Runge-Kutta schemes
• Interpolation for Runge-Kutta schemes

The following Maple worksheets can be downloaded.

They are all compatible with Classic Worksheet Maple 10.

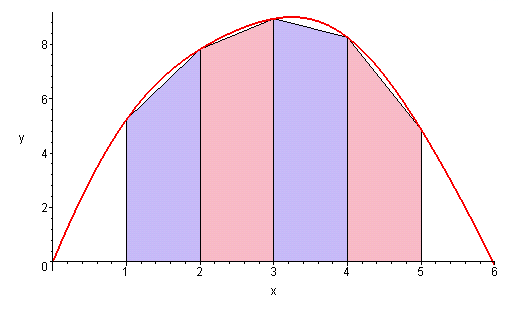
The trapezoidal rule - trapezoid.mws

• Description of the trapezoidal rule.
• A procedure for illustrating the trapezoidal rule graphically: drawtrap.
• Use of the procedure trapezoid in the "student" package.
• A procedure for performing the trapezoidal rule iteratively: trap.

Simpson's rule - simpson.mws

• Derivation of Simpson's rule.
• Use of the procedure simpson in the "student" package.
• A procedure for performing Simpson's rule iteratively: simp.

Applying Simpson's rule adaptively - adaptsimp.mws

• A preliminary adaptive procedure using Simpson's rule
• A procedure for performing Simpson's rule adaptively: SPint

Error analysis for the trapezoidal rule and Simpson's rule - simperr.mws

• An estimate for the error of the trapezoidal rule 
• An estimate for the error of Simpson's rule.

Simpson's rule for unequally spaced data points - simpint.mws

• A version of Simpson's rule for unequally spaced data points.
• A procedure for applying Simpson's rule to numerical data: gensimp
• "Indefinite" numerical integration via parabolic interpolation.
• A procedure to perform "indefinite integration" for numerical data: simpinterp

Newton-Cotes rules - NCint.mws

• Constructing Newton-Cotes Integration formulas
• Compound Newton-Cotes formulas
• A procedure for performing Newton-Cotes rules adaptively: NCint
  There are "built-in" coefficients for rules with an even number of intervals (odd number of points).
  There is an option to display the points used in evaluating the integral along a graph of the integrand.

Gauss-Legendre quadrature I - gauss.mws

• An introduction to Gauss integration formulas
• The Gauss 3-point rule
• Legendre polynomials
• Legendre polynomials as a "coordinate system" for polynomials
• Gauss integration formulas via Legendre polynomials
• A more convenient formula for the weights
• Computation of Gauss-Legendre nodes and weights

Gauss-Legendre quadrature II - GLint.mws

• A procedure for performing Gauss-Legendre quadrature adaptively: GLint
  There are built in abscissas and weights, which can be used up to a precision of 40 digits.
  GLint can refine the abscissas and weights to a higher precision if required.
  There is an option to display the points used in evaluating the integral along a graph of the integrand.

Gauss-Kronrod quadrature - kronrod.mws

• The basic idea of Kronrod extensions
• Extension of Gauss-Legendre integration formulas
• Calculation of nodes and weights for the 7 to15 node Gauss-Kronrod extension
• A preliminary routine for 7-15 Gauss-Kronrod integration
• Procedures for constructing Gauss-Kronrod nodes and weights

A procedure for performing Gauss-Kronrod quadrature - GKint.mws

• The basic idea of adaptive Gauss-Kronrod integration
• A procedure for performing Gauss-Kronrod quadrature adaptively: GKint
  There are built in abscissas and weights, which can be used up to a precision of 40 digits.
  There is an option to display the points used in evaluating the integral along a graph of the integrand
• Solving equations involving integrals.
• An arc length example

Chebyshev polynomials and Chebyshev series - chebfit.mws

• Definition of Chebyshev polynomials
• Properties of Chebyshev polynomials - orthogonality relations
• Expressing a polynomial as a Chebyshev sum
• An alternative method for calculating Chebyshev coefficients
• Chebyshev series
• Example: the Chebyshev series for exp(x)
• A procedure for computing Chebyshev polynomial: chebseries

Clenshaw-Curtis quadrature - CCint.mws

• Clenshaw-Curtis integration formula
• A basic procedure for Clenshaw-Curtis quadrature using Chebyshev series of fixed length
• A procedure for performing Clenshaw-Curtis quadrature iteratively: CCint

Romberg integration - romberg.mws

• Iterated application of the trapezoidal rule
• The Romberg triangle . . preliminary procedures for Romberg integration
• A procedure for performing Romberg integration: RBint

Comparison of methods of numerical integration - compare.mws

• Using Maple's evalf/Int scheme for numerical integration.
• Maple's numerical integration procedures available through evalf/Int
• An interface for the various numerical integration XXint routines: quad/int

Numerical integration of functions of varying "smoothness" - smooth.mws

• Integrating a succession of progressively smoother functions.

Numerical integration procedures - intg.zip

Data for the Gauss-Kronrod integration procedure GKint - GKdata.zip

Top of page

Main index